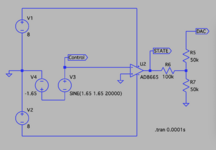
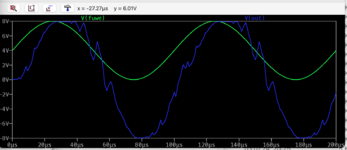
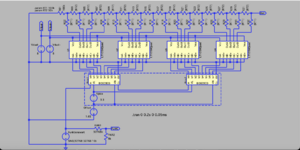
Ich hab' noch ein wenig weiter experimentiert. Mein Ziel ist es, ein DAC-Projekt mit dem Raspberry Pi Pico zu entwickeln. Das Herzstück ist natürlich der DAC daselbst. Die DAC-Widerstands-Logik hatte ich schon länger auf einem Blatt zur Simulation errichtet, das ist eigentlich keine Kunst sondern nur eine reine Fleißarbeit.
Wenn man jetzt so einen DAC mit 8 Bit Auflösung macht, wird man noch nicht allzu sehr gefordert. Über einen Internet-Kontakt bin zu einem Schaltungs-Entwurf für einen Raspberry Pi Pico gekommen, der eine Auflösung von 22 Bit ermöglicht. Weil mich das Geschehen interessiert und ich noch einen Retro-Röhrenverstärker bei etwa 70% (Halb-)Fertigstellung hier liegen habe, war die Aussicht auf einen Funktionsgenerator, den man mit einem solchen Mikrocontroller realisieren kann, schon sehr verlockend.
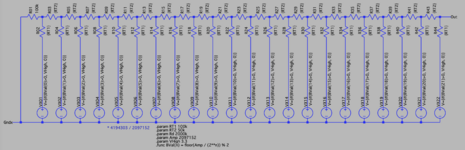
Ich hab' dann mal angefangen die DAC-Widerstands-Logik für die Simulation herzurichten. Das war ja noch relativ harmlos. Die Widerstandswerte lassen sich mit diesen zwei Parameter gemeinsam bestimmen:
.param RT1 100k
.param RT2 50k
Schwieriger war schon die Aufgabe, das Gesamtwerk dazu zu bringen, dass alle Bitzweige sich nach einem gemeinsamen Wert ausrichten, um damit die Amplitude bestimmen zu können. Jeder T-Zweig der Widerstandslogik ist an einen GPIO des Raspberry Pi Picos angeschlossen. Folglich kennt dieser Anschlusspunkt nur zwei Zustände: Bei logisch LOW den Pegel 0 V bzw. bei logisch HIGH den Pegel 3,3 V. Es lag also nahe zu diesem Zweck und Behufe solche Spannungsquellen des Typs
Arbitrary behavioral voltage source (wird mit bv ausgewählt) mit der Aufgabe zu betrauen.
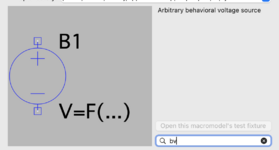 V=f()
V=f() steht in der Mathematik für eine Lösung, die über eine Funktion erfolgt. Die hab' ich dann auch hier angewendet:
.func BVal(n) = floor(Amp / (2**n)) % 2
- BVal, der Funktionsname entsteht aus der Kategorie-Kennung B für diese Art der Spannungsquellen und Val als Abkürzung für Value.
- n, ist ein Übergabeparameter für die Bitposition (0, 1, 2...), die ausgewertet werden soll.
- floor, der Begriff stammt aus der Mathematik und Informatik und bezieht sich auf die Funktion, die den größten ganzzahligen Wert zurückgibt, der kleiner oder gleich einer gegebenen Zahl ist. Die Verwendung von floor ist hier angebracht, weil LTspice intern mit Gleitkommazahlen rechnet.
- Amp, ich hatte keine bessere Abkürzung gefunden, nach dem Pfeife dieses Parameters sollen sich alle 22 Bitauswertungen richten. Über .param Amp 2097152 konnte ich z.B. einen Wert vorgeben, um die DAC-Widerstands-Logik zu testen und zu erfahren, was am Ende herauskommt.
- 2**n, bedeutet nichts anderes 2 hoch n und berechnet den Dezimalwert, der durch diese Bitstelle repräsentiert wird, wenn das Bit logisch HIGH ist.
- % ist der in LTspice nicht dokumentierte Modulo-Operator, der viele Sorgen bereitet hat.
Soweit die Funktion. Am Einsatzort wird die Funktion noch mit einer
if-then-else-Anweisung verknüpft,
if steht da noch,
then und
else muss sich jeder denken. Das Ergebnis der Funktion ist entweder 0 oder größer 0. Bei 0 bleibt es auch bei 0, bei >0 wird der Wert des Parameters
VHigh, in dem Falle 3,3 V ausgegeben.
V={if(BVal(0)>0, VHigh, 0)}
.param VHigh 3.3
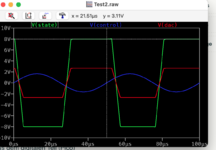
Also, mit dieser Schaltung könnte man schon mal was simulieren, aber es war noch nicht zufriedenstellend. Der Parameter
Amp ließ sich trotz guten Zuredens einfach nicht überreden, einer anderen Funktion zu folgen. Denn das wäre ein Nahziel gewesen, um später die Amplitude und Frequenz vorzugeben, um so z.B. eine Sinuskurve zu generieren.
Es gibt noch ein paar mehr Fallstricke in LTspice, ich glaub', ich hab' einige davon in diesem Zusammenhang kennen gelernt.
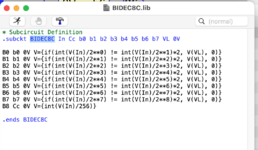
Auf der Suche nach einer Umgehung der großzügig ausgelegten Fallstricke bin ich mal wieder auf die Idee gekommen, einen Baustein zu kreieren. Aber dieses Mal nicht auf dem klassischen Wege, sondern direkt durch Eingabe in den Texteditor.
B0 b0 0V V={if(int(V(In)/2**0) != int(V(In)/2**1)*2, V(VL), 0)}
- B0, ein Gerät (Device), in dem Falle ein Arbitrary behavioral voltage source, erkennbar an dem Kennbuchstaben der Kategorie.
- b0, der Anschlusspin mit dem das Gerät die Verbindung zur Außenwelt aufrecht erhält und so die Spannung an den T-Zweig des DAC liefern soll.
- 0V, der zweite Pol des Gerätes und gleichzeitig ein ganz wichtiger, denn der muss nach "draußen" geführt werden, weil es sonst keinen Potentialbezug gibt.
- V=, hier wird die Funktion definiert, die dafür sorgt, dass der Anschluss b0 auch mit einem Wert versorgt wird.
Bleibt noch die Funktion für
b0 zu erläutern:
V={if(int(V(In)/2**0) != int(V(In)/2**1)*2, V(VL), 0)}
Wenn die Prüfbedingung wahr ist, dann wird
V auf den Wert gesetzt, der am Baustein-Eingang
VL verfügbar ist, sonst 0.
Zugegeben, das ist ein bisschen tricky, aber mir scheint es eine wirksame Art zu sein, die nur in seltenen Fällen bei LTspice verfügbare Modulo-Operation wirkungsvoll zu umgehen.
Die Zeilen für die Geräte
B1..B7 folgen dem gleichen Muster.
Die Zeile B8 ist wieder eine Besondere:
B8 Cc 0V V={int(V(In)/256)}
- B8, gleiches Gerät wie bei B0
- Cc, ähnlich wie bei b0, weil gleiche Funktion, aber auf einer anderen Berechnung beruhend.
- 0V, hatten wir schon mal, wie oben.
- V=, dieses Mal eine simple Division durch 256. Das wird dafür gemacht, weil der Baustein kaskadierbar ist. Da Cc über das Funktionsergebnis bei V= versorgt wird, kann so der nächste Baustein bei In mit dem für den Gebrauch korrigierten Wert versorgt werden. Der Baustein BIDEC8C dekodiert ausschließlich Werte von 0..255, daher werden die Werte für jeden kaskadierten Baustein entsprechend herunter geteilt.
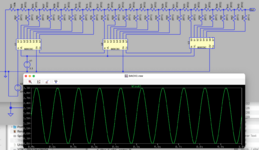
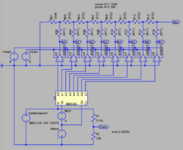
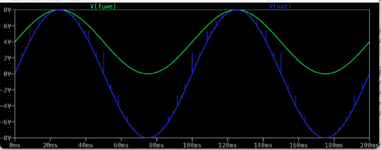
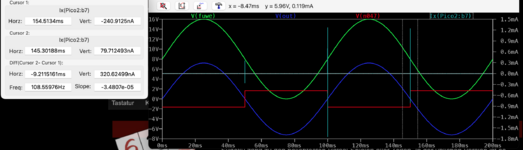
Das ist nun der erfolgreiche Einsatz des Bausteins. Kaskadiert in Serie um die Auflösung von 22 Bit abzudecken. Also, mir gefällt die Sinuskurve, die hier zur Demonstration des DACs mit dieser echten Auflösung in dem Plot produziert wurde. Zumindest das Simulationsergebnis belegt eindeutig die richtige Dimensionierung.
VG